elkiselee 2016-03

CAD로 재면 너무 쉬워요 ㅋㅋ

미니TM 2016-03

예  제 기억으로도 CAD면 한방에 해결 되는 것으로 알고 있는데
회사에 라이센스도 없고..
있어도 쓸줄 모르는... 뭐 그런 상황입니다. 흑흑.

간장게장 2016-03

구면좌표계
https://goo.gl/Z8QLbk

이걸참조하세요.

--------------------

가령

직교좌표계 P1(x1,y1,z1)
x1 = 0
y1 = 0
z1 = r
인 위치에서

반지름을 유지하면서 z축에서 theta만큼 x축에서 phi만큼 돌아간 점 P2(x2,y2,z2)

x2 = r sin(theta) cos(phi)
y2 = r sin(theta) sin(phi)
z2 = r cos(theta)

점 P1과 P2간의 거리는

square_root( (x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2 )


r, theta, phi 아는 값이면 P2의 좌표가 나오고, P1과 P2의 거리가 계산됩니다. 계산은 엑셀 같은 것으로 하면 되고요.

미니TM 2016-03

구면좌표계. 정확한 용어를 몰라 저런걸 못찾았네요. --;;

말씀하신대로 처음 위치는 점 P0 (0 0 0 )에서 점 P1인데 각도가 틀어져 P1에서 P2로 이동..

그 뒤에는 P0 - P2를 기준으로 해서 틀어진 걸 계산...

봐도 복잡해지네요...

간장게장 2016-03

직선에서 한쪽 끝점을 (0,0,0)이라고 치고 다른 쪽 끝점 P1을 (0,0,r)이라고 치고
(0,0,0)은 고정한 채 P1을 theta, phi만큼 돌린 점 P2(x2,y2,z2)를 생각하면 됩니다.

반지름이 1000이고 z축에서 1도 x축에서 3도 틀어진 경우라면 P1에서 P2로 움직인 거리는 5.5555로 계산되는군요.

엑셀로 quick and dirty로 만든 것을 자료실에 올려두겠습니다. 한시간 뒤에 지움
이걸 변형시켜 사용하세요.

미니TM 2016-03

음 열심히 보고 분석하고 있습니다.
현재 말씀하신 것중에 정의된 것이 세타값은 z축이 틀어진 각도이고, 파이값은 x축이 틀어진 각도이죠?

현재 오차를 구해야하는 것이.. 그림1과 2가 서로 다른 축을 기준으로 하는 것인데 제가 설명이 부족했네요.
응용을 하면 될 것 같은데.. 일단 계산 해봐야겠습니다!
감사합니다.

무아 2016-03

보통 이정도면 (y축의 기울어짐이 미미하다면) 그냥 x 값을 써도 무방하지 않을까요? 공차 이내에 들어온다면.. 그럴 공산이 커 보이는데요 ^^

미니TM 2016-03

예. 실제로 계산을 해보니 y축이 틀어지는 경우는 좀 미미하긴 한데..
(0,0,0)에 있는 녀석과 P1에 있는 녀석이 완전히 직선을 이뤄졌다는 보장이 없어져버려서...
P1이 살짝 틀어진 경우에는 오차가 상당히 클 것 같습니다... 목표가 40000까지의 거리에서 차이를 비교해야되서요..

간장게장 2016-03

의미를 제가 잘못 알았던것 같습니다.

구면 좌표 생각할 거도 없이 직각좌표상에서

C1(0,0,0)에서 거리 r1 떨어진 곳에 있는 점 P1(r1,0,0)이 y축 방향으로 theta만큼 회전하여 P2로 갔다고 하면 P2의 좌표는
x2 =  r1 cos(theta)
y2 = r1 sin(theta)
z2 = 0

P1~P2 변위는

sqrt( ( r1 - r1 cos(theta) )^2 + ( r1 sin(theta) )^2 ) = r1 * sqrt( 2 - 2 cos(theta) )

가령 r1이 1000이고 theta가 1도(1/180 radian)라면 변위는 5.5555

그런데 P2가 다시 원점이 아닌 P2로부터 거리 r2 떨어진 C2라는 점을 중심으로 phi만큼 회전하여 P3라는 점으로 이동했다면
P2~P3 변위는 r2 * sqrt( 2 - 2 cos(phi) )

가령 r2가 50이고 phi가 3도(3/180 radian)라면 변위는 0.8333

이 변위 값은 C2가 어느 위치이건 phi가 어느 방향으로 회전을 했건 마찬가지입니다.

P1~P3의 변위를 알려면 두번째 회전의 중심 C2의 위치와 phi가 어느 방향으로 회전을 한 것인지를 알아야 계산할 수 있습니다.

그러나 어느 한계에 있는 지는 알 수 있습니다.

P1, P2, P3 세 점으로 이루어지는 삼각형에서 삼각형 두변의 합은 다른 한변보다 크기 때문에

( P1~P2 + P2~P3 ) > ( P1~P3 )


어느 점을 중심으로 어느 방향으로 회전을 했건 간에 두번 세번의 회전이 있을 때 전체 변위는 각각의 변위를 합한 것보다는 작다는것이죠.

반지름 : r
회전 각도 : theta

이러면 변위는

r * square_root( 2 - 2 cos(theta) )

요걸로 계산하여 몽땅 합쳐주면 실제 변위는 그것보다는 작은 값이 됩니다. 최종 오차는 이런저런 오차를 단순 합산한 것이 한계치


변위의 한계가 아니라 정확한 값을 알려면 물론 어느 점을 중심으로 어느 방향으로 회전했는지를 알아야겠죠.

미니TM 2016-03

감사합니다.
계속 삼각함수로 까대기 하고있었는데 좀 가닥이 잡히네요.
일단 또 해봐야지요... 흑흑...

무아 2016-03

질문이 좀 이해가 안되는데
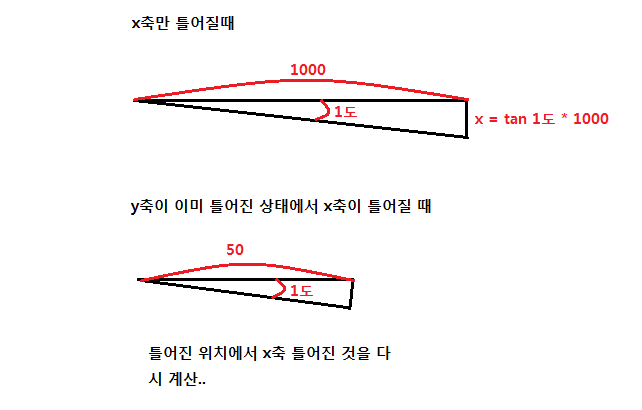
위에 두 그림에서 하나는 1000, 하나는 500. 왜 다른 거죠?

미니TM 2016-03

헤헤.. 글이랑 그림이 좀 그렇습니다..

1번 그림은 한축만 틀어진 것이고
2번 그림은 1번을 진행하기 전에 이미 2번과 같이 틀어진 상태에서 다른 축으로 1번 그림으로 진행하는 것입니다.

현재 상황이 O0 (0, 0, 0) P1(0, 0, 50)을 잇는 직선이 있고 P1(0, 0, 50)에서 C1(1000, 0, 50)까지의 90도 꺽인 직선이 있습니다.
1번은 P1에서 C1까지인데 P1을 중심으로 y축이 틀어졌을 경우의 그림이고
2번은 O0에서 P1까지인데 O0을 중심으로 x축이 틀어졋을 경우의 그림입니다.
최종은 2번이 진행되어 P1`이 (0, 1, 49)의 위치로 간 상태에서 P1`에서 C1`(1000, 1, 49) 까지가는데  이게 또  y축이 틀어졌을 경우 원래 도달 위치인 C1에서 얼마나 틀어지냐 이것입니다.
O0에서 P1까지의 길이는 50 고정이고 P1에서 C1 까지는 거리가 아닌 (1000, y, z) 까지 도달해야 합니다.