쪽팔리면 질문하지 맙시다. 소중한 답변 댓글을 삭제하는건 부끄러운 일 입니다
libfftw를 이용하여 주파수 분석을 하려는데
fftw_plan_dft_r2c_1d() 함수에
N개의 입력을 넣었다면
N/2 + 1 개의 출력이 나옵니다.
DFT에 의해서 N/2가 되는건 알겠는데 1은 어떤 정보가 나오는지 모르겠습니다.
혹시 +1의 신호가 어떤 것인지 참고할 만한 문서가 있을까요?
+
이미지 추가
딸 다섯 아들 하나 아빠 (큰 딸, 작은 딸, 왕큰 딸, 앵무새, 암 뭉뭉이, 수 뭉뭉이) - minimonk.net




Here, n is the “logical” size of the DFT, not necessarily the physical size of the array. In particular, the real (double) array has n elements, while the complex (fftw_complex) array has n/2+1 elements (where the division is rounded down). For an in-place transform, in and out are aliased to the same array, which must be big enough to hold both; so, the real array would actually have 2*(n/2+1) elements, where the elements beyond the first n are unused padding. (Note that this is very different from the concept of “zero-padding” a transform to a larger length, which changes the logical size of the DFT by actually adding new input data.) The kth element of the complex array is exactly the same as the kth element of the corresponding complex DFT. All positive n are supported; products of small factors are most efficient, but an O(n log n) algorithm is used even for prime sizes.
https://www.fftw.org/fftw3_doc/One_002dDimensional-DFTs-of-Real-Data.html#One_002dDimensional-DFTs-of-Real-Data
번역을 돌려봐도 무슨 소리인지 모르겠습니다
아무튼 실수(real number)를 DFT 하면 N/2+1로 나오는데
0은 이상하게 큰 값이 하나 튀어나오고 1~N/2+1 까지 값이 나오는 것 같은데
0이 FFT 연산에 의한 값이냐(즉, 0Hz에 대한 계산 결과) 이런게 궁금합니다.
일단 r2c 함수에 r값으로 0~1 사이로 normalize 했는데도
dft 결과의 0 번 인덱스에 900,000 근처의 값이 들어가는걸 보면.. 원본 값을 모르는데 얻어걸린 값인지(원본 데이터가 +-900,000 범위로 나옴)
어떻게 해석해야 할지 모르겠습니다.
(원본 데이터가 +-900,000 범위로 나옴) 이런데 0 번 인덱스에 900,000 근처의 값이 들어있다? 뭔가 이상한데요
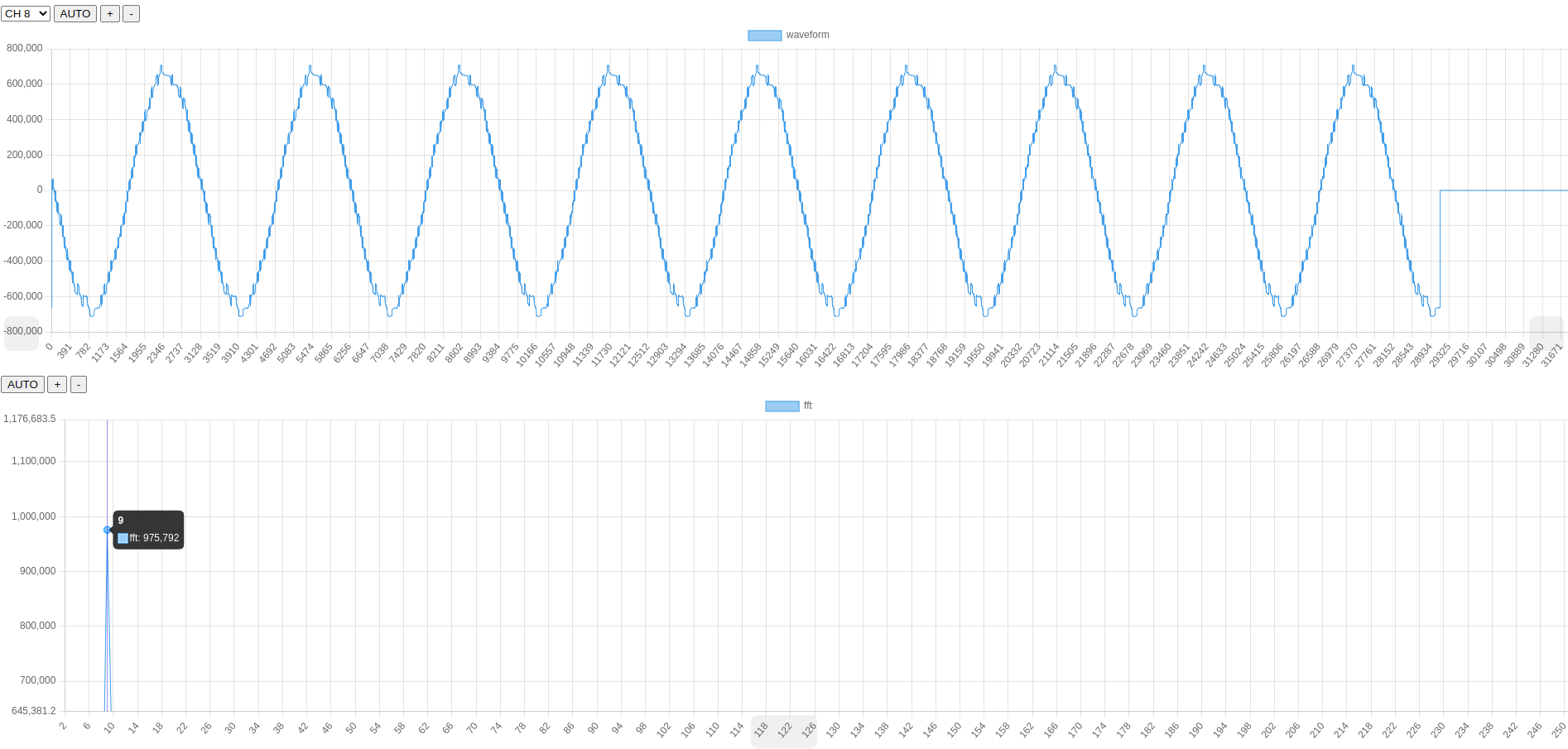
이미지 추가했는데 원본 신호는 위와 같고
아래는 fftw 라이브러리로 처리한 결과입니다. 0번째 값이 이상하다고 생각해서 0으로 처리했고
fft 입력값은 800,000 / 16777216(24bit) 로 나누어서 0~1 사이의 실수로 변환하였습니다.
그러니까 출력이 복소수로 나오는데
ai+b 에서
sqrt(a^2 + b^2) 로 amplitude로 변환한다고 해서 했는데 수식이 이상한건지 강도가 975,000 정도로 나오네요
복소수의 크기 계산식이 잘못되었는지 단계별로 검증해봐야 할 것 같습니다 ㅠㅠ
http://www.ktword.co.kr/test/view/view.php?no=3725
천천히 읽어는 보겠지만.. 전기/전자 전공이 아니라 이해하기 쉽지가 않네요 ㅠㅠ
stackoverflow
https://stackoverflow.com/questions/36637727/fftw-library-what-is-the-output-size-of-fftw-plan-dft-r2c-1d
http://www.fftw.org/fftw3_doc/
http://www.fftw.org/fftw3_doc/Real_002dto_002dReal-Transform-Kinds.html#Real_002dto_002dReal-Transform-Kinds
i0 is 0 because you're using real data , so it isn't stored in out.
stackoverlfow 보면 위와 같이 써있는데 그냥 1~N/2+1 까지 쓰면 될 것 같네요
감사합니다.
The 0 Hz component is in bin 0.
This is all covered in the FFTW manual.
라는 말이 있는 거 보니 +1 은 DC 성분 이네요. 정확히는 0 번째 인덱스겠죠.
"complex outputs for N real inputs" 출력이 복소수라서.
위대하신(?) chatGPT 님께서는 아래의 대답을 내어주셨습니다.
다만.. stackoverflow나 이거나.. 번역해줘도 이해를 못하겠다는게 함정이네요.
FFTW 라이브러리에서 Fast Fourier Transform (FFT)를 적용하면, 길이가 N인 실수 입력 데이터에 대해 복소수 출력 데이터 N/2+1개가 생성됩니다. 이는 FFT 알고리즘이 동작하는 방식 때문입니다.
FFTW에서 사용되는 FFT 알고리즘은 "real-to-complex" FFT라고 불리며, 실수값 입력 데이터를 복소수값 출력 데이터로 변환합니다. 이 알고리즘은 실수값 신호의 푸리에 변환의 대칭성(symmetric) 특성을 활용합니다. 구체적으로, 실수값 신호 x(t)의 푸리에 변환 X(f)은 X(-f) = conj(X(f)) 라는 복소수 공액대칭성(complex-conjugate symmetric)을 만족합니다. 여기서 "conj"는 복소수 공액(conjugate)를 의미합니다.
이 대칭성 특성 때문에 FFT 알고리즘의 출력값 중 절반은 중복되는 값이며, 나머지 절반은 이 중복된 값들로부터 계산될 수 있습니다. 구체적으로, 0부터 N/2까지의 주파수 대역에서는 고유한 출력값이 존재하며, N/2+1부터 N-1까지의 주파수 대역에서는 대응하는 1부터 N/2-1까지의 주파수 대역의 복소수 공액값을 계산하여 구할 수 있습니다.
따라서 FFTW는 연산 시간과 메모리를 절약하기 위해, 0부터 N/2까지의 주파수 대역에 대한 고유한 출력값과, N이 짝수인 경우 주파수 N/2에 대한 출력값을 계산합니다. 이렇게 계산된 출력값의 총 개수는 N/2+1개가 됩니다.
0Hz 라고 하면 AC가 아닌 DC 성분으로 전체 신호가 만약 +2000 만큼 떠있다면 2000이 기록되는걸까요?
>>0Hz 라고 하면 AC가 아닌 DC 성분으로 전체 신호가 만약 +2000 만큼 떠있다면 2000이 기록되는걸까요?
네.
0 + N/2 주파수 니까 총 N/2+1 개이며
0Hz에는 신호의 DC 성분(0Hz) 내용이 있다고 이해하도록 하겠습니다.
감사합니다!
너무 어렵습니다 ㅠㅠ
나중에 다시 프로그램 수정해서 돌려보고 분석해서 추가글 쓰도록 해보겠습니다.
감사합니다
3축 제어를 하며 물성 측정하는 소프트웨어를 개발한 적이 있는데 (여전히 업그레이드하며 판매중인)
의뢰를 주신 대표님이 저보고.. 왠만한 화학과 대학원생보다 났다고 하더군요. 측정 및 분석 툴을 만드는 것인데 내용을 이해 못하면 툴을 만들지 못해서..
항상 다른 분야를 이해하게 하는 역할을 강제 당하는 느낌입니다.
아직도 끝나지 않은 레이저 분광기랑, 진동 데이터 획득 하여 주파수 분석하는 것 까지 이해하려니 머리가 아프네요.
핑계이긴 한데.. 전산학 계열 출신이라 여기 분들 대부분이 전기/전자 출신인데
정작 라이브러리 써본사람은 없어서 제가 열심히 구르는 중입니다. 데구르르르르
+
갈려나갔을 무명의 화학과 대학원생에게 묵념을..
왠지 Signal Processing 이라는 원서를 하나 정독하고 있을 미래가 보입니다. 흐흐흐..
만들다 보니 웹 오실로스코프네요
특정 주파수에서 피크가 잘 뜨네요. 정현파를 넣으면 저렇게 나오죠.
어떤 값인지 이해를 못해서 q/a에 올리게 되었네요
잘 정규화 했다면 주파수가 있는 부분의 크기값도 1을 넘지 않을텐데
일단은 double 형이다 보니 amplitude를 int 형으로 표현하려고 * 1000 해둔걸 까마득이 잊고 있었습니다. 하하하하 ㅠㅠ