안녕하세요
머신러닝 사용기 마지막 강좌 입니다.
이번 강좌는 http://hunkim.github.io/ml/ 의 강좌를 보고 진행 하였습니다.
소스코드는 http://pythonkim.tistory.com/notice/25의 자료에 도움을 받았습니다.
지난 번에는 머신러닝을 통해 90% 의 인식률을 보였습니다.
간단한 코드로 학습이 가능하다는 것을 보여준 예제였는데요
학습 모델을 그려보면 아래와 같습니다.
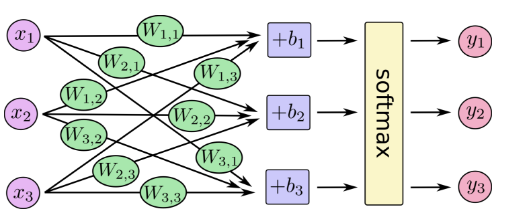
X(이미지 픽셀 정보)를 입력 받아서 이에 해당하는 Weight(W)와 Bias(B)를 학습 하는 것이지요
우리가 학습했던 모델은 이것과 동일하지만 차이가 있다면
X의 개수가 28X28 = 784 였고, Y의 개수가 10 이었던 것 입니다.
우리가 학습시킨 파라메터의 숫자는 W 7840개, B 10개 해서 7850개 입니다.
속을 잘 들여다 보면 결국 선형 회귀 방법의 응용이고 학습 층이 1층에 불과합니다.
오늘은 이 층을 쌓아서 성능이 개선되는 것을 살펴보겠습니다.
사실 층을 쌓게 된 이유와 층을 쌓아서 발생한 문제점, 그리고 해결방법들에 대한 이야기 들이 있지만
오늘은 건너뛰고 단순히 층을 쌓고 학습을 시켜보겠습니다.
오늘 학습시킬 모델의 모습은 아래와 같습니다.

보시는 것처럼 여러 층으로 발전 했습니다.
중간에 RELU는 Activation function 으로 입력을 받아 이를 활성화 할지 여부를 결정하는 함수 입니다.
수학적으로는 아래와 같은 행렬 연산이 됩니다.
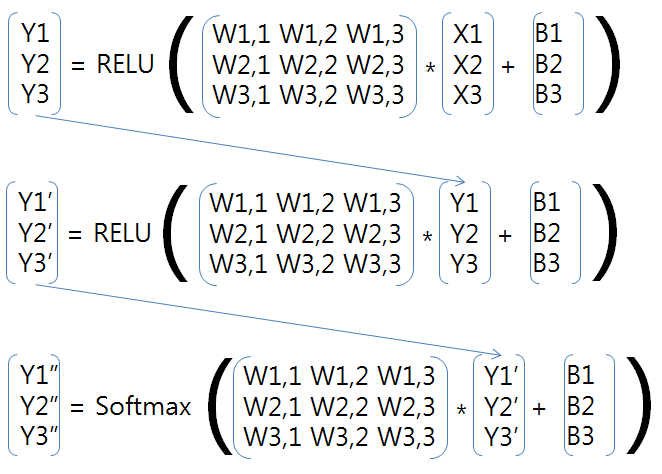
층의 개수와 크기는 원하는 대로 생성 할 수가 있습니다.
단 행렬 곱을 해야 하게 때문에 앞의 층의 출력과 뒤의 층의 입력이 같은 개수를 가져야 합니다.
이번 예제에서는 입력이 (784,256) ->(256,256)->(256,10) 인 학습 층으로 해 보겠습니다. (입력,출력)
이를 코드로 구현해 보면 아래와 같습니다.
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
learning_rate = 0.001
training_epochs = 15
batch_size = 100
display_step = 1
X = tf.placeholder(tf.float32, [None, 784]) # mnist data image of shape 28*28=784
Y = tf.placeholder(tf.float32, [None, 10]) # 0-9 digits recognition => 10 classes
W1 = tf.Variable(tf.random_normal([784, 256]))
W2 = tf.Variable(tf.random_normal([256, 256]))
W3 = tf.Variable(tf.random_normal([256, 10]))
B1 = tf.Variable(tf.random_normal([256]))
B2 = tf.Variable(tf.random_normal([256]))
B3 = tf.Variable(tf.random_normal([ 10]))
L1 = tf.nn.relu(tf.add(tf.matmul(X, W1), B1))
L2 = tf.nn.relu(tf.add(tf.matmul(L1, W2), B2)) # Hidden layer with ReLU activation
hypothesis = tf.add(tf.matmul(L2, W3), B3) # No need to use softmax here
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(hypothesis, Y)) # softmax loss
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
init = tf.initialize_all_variables()
with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
_, c = sess.run([optimizer, cost], feed_dict={X: batch_xs, Y: batch_ys})
avg_cost += c / total_batch
if (epoch+1) % display_step == 0:
print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
print("Optimization Finished!")
correct_prediction = tf.equal(tf.argmax(hypothesis, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print("Accuracy:", accuracy.eval({X: mnist.test.images, Y: mnist.test.labels}))
결과는 아래와 같습니다.
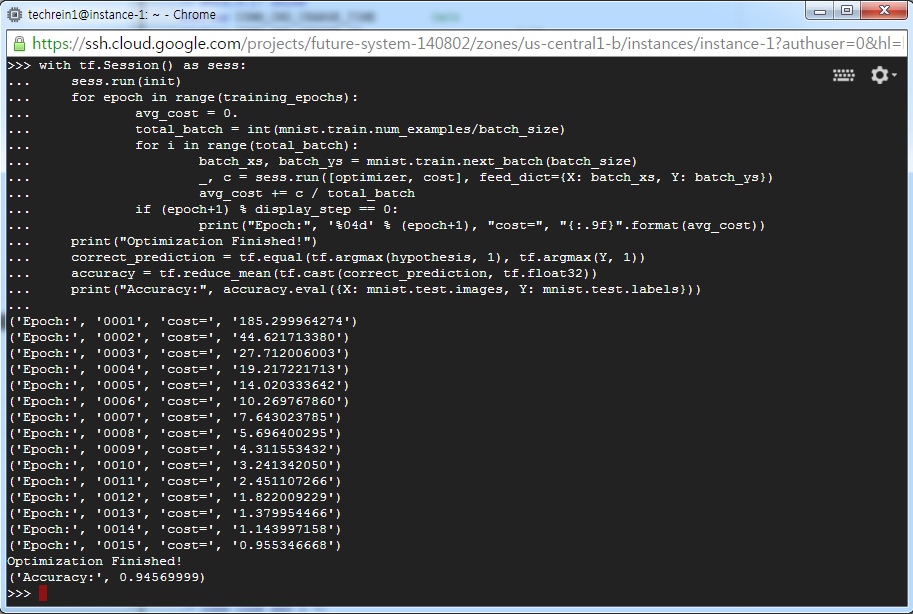
94.5%의 인식률로 이전보다 3%정도 가량 향상된 결과를 보입니다.
코드를 살펴보겠습니다.
입력으로 들어오는 28X28의 공간과 출력으로 나가는 10개의 공간을 정의 합니다.
X = tf.placeholder(tf.float32, [None, 784]) # mnist data image of shape 28*28=784
Y = tf.placeholder(tf.float32, [None, 10]) # 0-9 digits recognition => 10 classes
학습할 Weight를 선언합니다. Weight의 숫자는 각 층에 들어오는 입력의 숫자 X 출력의 숫자가 됩니다.
W1 = tf.Variable(tf.random_normal([784, 256]))
W2 = tf.Variable(tf.random_normal([256, 256]))
W3 = tf.Variable(tf.random_normal([256, 10]))
학습할 Bias를 선언합니다. Weight의 숫자는 각 층에서 나가는 출력의 숫자입니다.
B1 = tf.Variable(tf.random_normal([256]))
B2 = tf.Variable(tf.random_normal([256]))
B3 = tf.Variable(tf.random_normal([ 10]))
각 층간의 관계를 정의 합니다.
L1 = X*W1+B1, L2= L1*W2+B2, hypothesis = L2*W3 +B3 으로 정의 됩니다.
L1 = tf.nn.relu(tf.add(tf.matmul(X, W1), B1))
L2 = tf.nn.relu(tf.add(tf.matmul(L1, W2), B2)) # Hidden layer with ReLU activation
hypothesis = tf.add(tf.matmul(L2, W3), B3) # No need to use softmax here
학습은 코스트 값을 정의하고 이 코스트 값이 줄어드는 쪽으로 W,B를 변경시켜 나가는 과정입니다.
이전에는 Gradient Descendent 알고리즘을 사용했었는데 이번에는 AdamOptimizer를 사용했습니다. 방법은 다르지만 하는 일은 동일합니다. 코스트가 감소하는 방향으로 W,B를 조정해 주는 것 입니다.
셋팅을 마치고 모든 변수값을 초기화 합니다.
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(hypothesis, Y)) # softmax loss
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
init = tf.initialize_all_variables()
데이터의 크기가 크므로 데이터를 나누어 진행합니다.
데이터를 100개로 나누어서 1%의 데이터를 가지고 학습을 시키는 것을 15번(training_epochs) 진행합니다. 위에서 설정한 AdamOptimizer가 반복적으로 실행되면서 학습이 진행됩니다.
with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
_, c = sess.run([optimizer, cost], feed_dict={X: batch_xs, Y: batch_ys})
avg_cost += c / total_batch
if (epoch+1) % display_step == 0:
print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
print("Optimization Finished!")
맞은 케이스를 세서 정확도를 계산합니다.
correct_prediction = tf.equal(tf.argmax(hypothesis, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print("Accuracy:", accuracy.eval({X: mnist.test.images, Y: mnist.test.labels}))
이렇게 학습 층을 쌓아서 정확도를 향상 시킬 수 있습니다.
흔히 우리가 Deep learning이라고 불리는 것이 이 방법입니다.
여기서 초기값 설정과 Drop out 을 설정하면 97% 정도 까지 인식률이 향상되며
Convolution Neural network 를 적용하면 98~99% 의 인식률이 나옵니다.
각 층의 연결에 따라서 여러가지 방법들이 있으며
아직도 계속해서 새로운 방법들이 연구 되고 있습니다.
주마간산처럼 deep Learning을 살펴 보았네요
개인적으로는 시작할 때는 잘 몰랐지만 조금 살펴보고 나니 Machine Learning이 그렇게 어렵지 않다는 것을 알 수 있었습니다.
우리가 이러한 알고리즘을 직접 향상시키는 것은 쉽지 않겠지만 이렇게
잘 만들어져 있는 툴을 가지고 우리 생활에 적용하면 좋은 결과가 있을 것이라 생각합니다.
감사합니다.




실질적으로 응용하시는 작업도 잘 진행되는 것으로 생각됩니다.
목표에 접근하시는 것 같습니다. 화이팅입니다.
응원해 주셔서 점점 나아지고 있어요
관심있고 배우고 싶었는데...
혹 시즌2는 없나요? 요런거 좀더 응용하는...ㅎㅎ
저도 배우고 있는 중이어서요 :)
만들고 싶은게 있으신가요?
내 행동반경, 움직이는 시간등을 예측해서... 조언을 해주는...
개인 기상청이라고나 할까요..ㅎㅎ
개인의 위치 정보를 가지고 있다면 만드어 볼 수 있겠네요
어디서 들은건데 데이터를 충분히 모으면
특정시간의 사람의 위치를 90%정도 예측 가능하다고 하더라구요
입력값이 랜덤이라 안될것도 같은데...
혹 인간의 직관이 간과 할 수 있는 부분을(알파고 처럼..)
학습을 통해 발견할 수도?? ㅎㅎ
딥러닝은 패턴을 발견하고 학습하는 기법이기 때문이죠.
만약 로또 1등 예측을 한다면 ... 저도 바로 ...
좋은글 잘 읽었습니다. ^^